Abstract
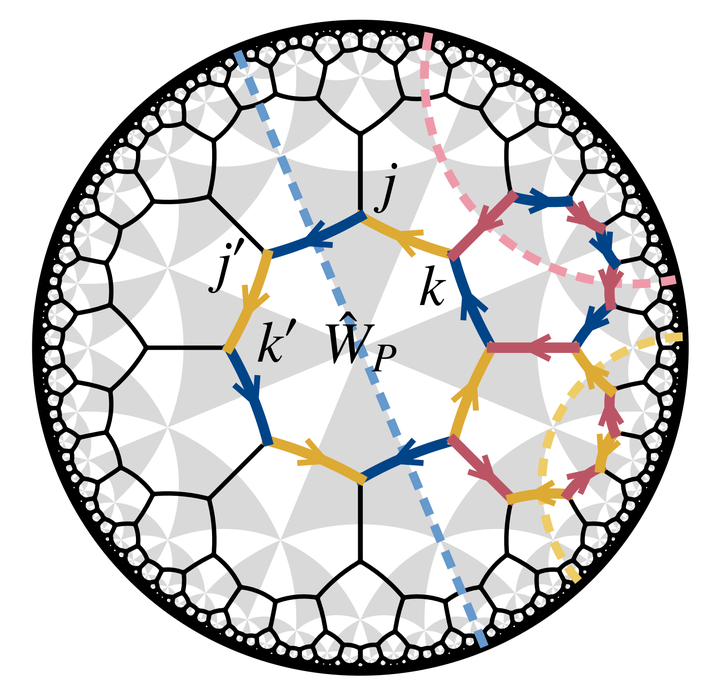
Hyperbolic lattices present a unique opportunity to venture beyond the conventional paradigm of crystalline many-body physics and explore correlated phenomena in negatively curved space. As a theoretical benchmark for such investigations, we extend Kitaev’s spin-1/2 honeycomb model to hyperbolic lattices and exploit their non-Euclidean space-group symmetries to solve the model exactly. We elucidate the ground-state phase diagram on the ${8,3}$ lattice and find a gapped $\mathbb{Z}_2$ spin liquid with Abelian anyons, a gapped chiral spin liquid with non-Abelian anyons and chiral edge states, and a Majorana metal whose finite low-energy density of states is dominated by non-Abelian Bloch states.
Type
Publication
Phys. Rev. Lett. 135, 076604 (2025)